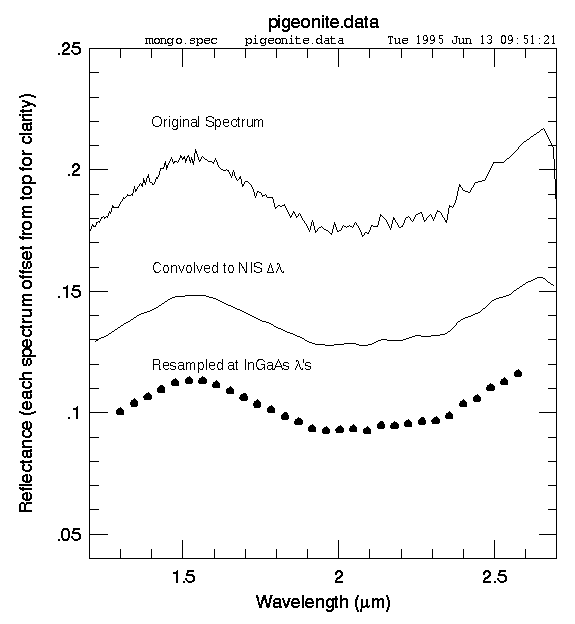
 Figure 1: Pigeonite spectrum used in InGaAs SNR Analysis (Clark et al., 1993)
Figure 1: Pigeonite spectrum used in InGaAs SNR Analysis (Clark et al., 1993)
NIS Calibration Report #5
Jim Bell; 5/20/95
Issue:
How will the expected poor SNR of the InGaAs detector (1.3 to 2.6 um) effect the detectability and discriminability of the types of mineral features we might see on Eros?
Methods:
(1) Assemble a small set of lab spectra of minerals of interest containing rather broad Fe2+ absorption bands around 2 um (pigeonite, enstatite) and rather narrow cation-OH absorption bands around 2.2 um (nontronite, montmorillonite).
(2) Also, generate some synthetic "perfect" 20%-deep absorption bands similar to ones seen in pure minerals.
(3) Convolve spectra in (1) and (2) to InGaAs resolution (R = 30 to 60 from 1.3 to 2.6 um).
(4) Resample spectra in (3) to typical InGaAs sampling (30 channels)
Examples of two minerals, enstatite and pigeonite, that have gone through this process are shown in Figures 1 and 2 below:
 Figure 1: Pigeonite spectrum used in InGaAs SNR Analysis (Clark et al., 1993)
Figure 1: Pigeonite spectrum used in InGaAs SNR Analysis (Clark et al., 1993)
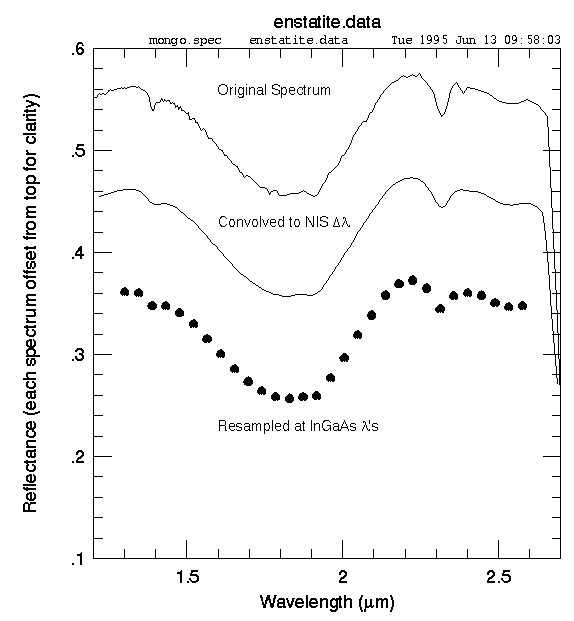 Figure 2: Enstatite spectrum used in InGaAs SNR Analysis (Clark et al., 1993)
Figure 2: Enstatite spectrum used in InGaAs SNR Analysis (Clark et al., 1993)
(5) Add random (Gaussian-distributed) noise to the spectra in (4) to simulate different SNR levels. For the real mineral spectra, the original SNR is ~ 100, so simulate SNR = 75, 50, and 20. The synthetic spectra are generated at SNR = 1000, so simulate at SNR = 500, 100, 75, 50, 20.
An example of this process performed on a synthetic 1.8 micron band spectrum is shown in Figure 3 below.
 Figure 3: Synthetic 1.8 micron spectrum with different amounts of added random
noise. The SNR of the spectra is shown to the right of each.
Figure 3: Synthetic 1.8 micron spectrum with different amounts of added random
noise. The SNR of the spectra is shown to the right of each.
Results:
Real Minerals:
The broad feature near 2 um (e.g., enstatite, pigeonite) is detectable even in SNR=20 data for the pure mineral phases; however, substantial errors in derived spectral parameters arise if SNR < 50, and detailed mineralogic characterization would be difficult for SNR < 100 in many cases.
An example of derived band parameters for the Enstatite 1.8 micron band is shown in Figure 4 below.
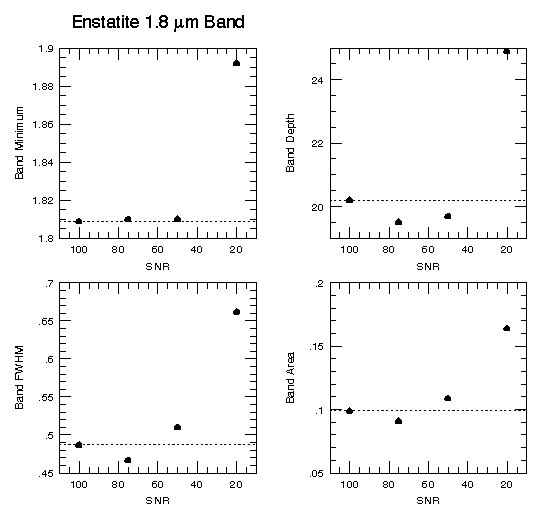 Figure 4: Derived parameters for band center, depth, width, and area for the
Enstatite 1.8 micron band assuming spectra of different SNR values. The dashed
line shows the actual values of each parameter (at infinite SNR)
Figure 4: Derived parameters for band center, depth, width, and area for the
Enstatite 1.8 micron band assuming spectra of different SNR values. The dashed
line shows the actual values of each parameter (at infinite SNR)
The narrow feature near 2.2 um, in montmorillonite (Al-OH) for example, is detectable as a 2-channel feature in most spectra of SNR > 50. However, detailed characterization of this band is difficult and depends on the particular fitting model to be used. A polynomial fit, for example, was able to consistently fit the SNR = 100 and 75 data. However, how well can you trust band fitting based on two channels??
Synthetic Spectra:
The broad feature near 2 um is once again detectable at all SNR values >= 20 tested. SNR=100 seems to be the magic point for being able to accurately model the broad 2-um band using my simple techniques.
The narrow bands near 2.2 um are again being characterized by only a few channels. However, the features can be detected even at SNR=20 in the pure minerals, although there is much "noise" that is also generated at the same spectral level. Reliable estimates of band parameters appear to require SNR >= 100 at least, although a quick analysis indicates that SNR > 250 would really be needed in order to get a handle on these narrow features at the poor InGaAs sampling.
An example of derived band parameters for the synthetic 2.2 micron band is shown in Figure 5 below.
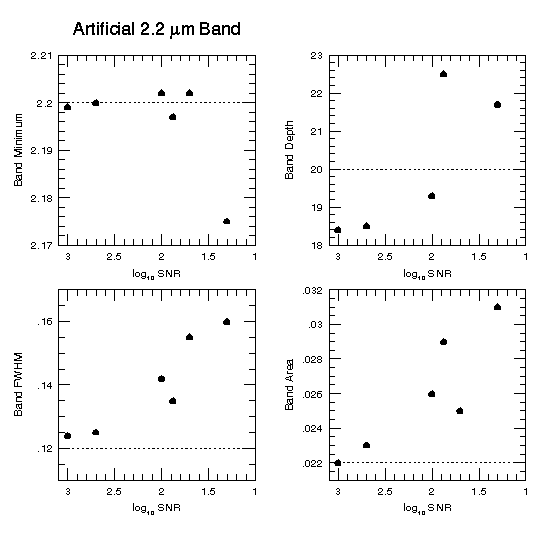 Figure 5: Derived parameters for band center, depth, width, and area for the
narrow synthetic 2.2 micron band assuming spectra of different SNR values.
The dashed line shows the actual values of each parameter (at infinite SNR)
Figure 5: Derived parameters for band center, depth, width, and area for the
narrow synthetic 2.2 micron band assuming spectra of different SNR values.
The dashed line shows the actual values of each parameter (at infinite SNR)
Summary:
If we can get SNR >= 100 for InGaAs, we should be able to detect and quantify at moderate accuracy the parameters of most of the spectral features we expect to see. If narrow absorption features are detected on Eros, we will need higher SNR values to assure ourselves of accurate band fitting. Based on the initial reports of the improved InGaAs performance by Jeff Warren and others, it appears that we should be just fine.
Note:
This analysis is demonstrative only. We will not see perfect bands on Eros, nor will we see (most likely) bands as deep as those in pure lab minerals. So these results represent best case, and we probably want to shoot for factors of two to five improvement in SNR (i.e, SNR > 200 to 500).